まずは全体像をつかもう
何を学ぶにしても,その全体像を知っておくというのはとても大事。
イン数はその名の通り中高数学の全範囲が対象だから,まずは小中高で学ぶ算数・数学のマップを見てほしい。
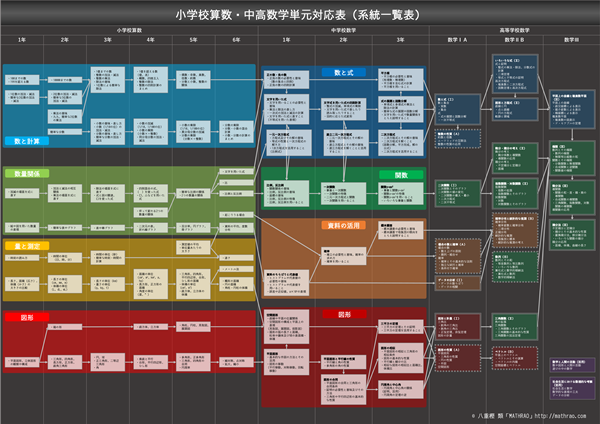
小学校算数・中学校数学・高等学校数学単元対応表(系統一覧表)
自分が何を学んできて,これから何を学ぶか確認できたかな?
習ったけど全然覚えてない内容はないかな?
こうやって全体像を眺めると,今までとこれからがどうやってつながっていくのかが分かりやすいはず。
同じ色が使われている部分は特に強くつながっているところだから共通して使う知識も多い,という視点も大事だよ。
イン数の目次
イン数は,以下のような順番で学習を進めていく。
- 集合と論証
- 正負の数と計算
- 文字式と計算
- 展開と因数分解
- 数
- 方程式と不等式
- 図形と計量
- 方程式と図形
- ベクトル
- 複素数平面
- 数列
- 関数
- 微分法
- 積分法
- 確率
- 統計
題名は堅苦しく見えるけど,中身の文章の表現はなるべく柔らかく,必要な部分は締めてメリハリをつけていくから安心してね。
最低限知っておいてほしい言葉
数学を学ぶ上で,これだけは覚えておいてほしい重要な用語がいくつかある。
それが,命題・証明・公理・公理系・公準・定義・定理・性質・公式・系・原理・法則。
多すぎ?
でも,これらは今後数学を学ぶときになんのことわりもなく出てくる用語だから,ここで一気に確認しておいてほしい。
最初から全てを暗記するのは大変だから,出てきたらここを見返してくれればいいよ。
命題(proposition)・証明(proof)
「命題」とは真偽のはっきりする文章や式のことで,その命題の真偽を一切の仮定なくはっきりさせることを「証明」という。
数学者は「これはこうなるんじゃないか?」というような仮説などを命題として,それを証明するということを続けてきた。
証明ができればその命題が新たな事実として認められ,そこからさらに新しい命題が作られ…のエンドレスリピート。
こうやって数学は発展してきたんだ。
ちなみに,命題や証明を公式に発表したものを論文という。
公理(axiom)・公理系(axiomatic system)・公準(postulate)
公理っていうのは,数学における大前提。
学校で学ぶ算数・数学もいくつかの公理に従っているんだけど,それを実感することは少ないかもしれないね。
「 $1+1$ と $2$ が等しい」ことや,「2つの点を結ぶことができる」といったことは当たり前に感じるかもしれないけど,きちんと公理に書かれてる。
数学っていうのはそれこそ一分の隙もない学問で,「たぶん」という言葉は禁句なのよ。
定義(definition)
命題や証明で新しい用語を使うときには,必ずその意味を明確にしなきゃいけない。
じゃないと人によって捉え方が違うなんてことになりかねないからね。
逆に言えば,同じ用語でも命題や証明が違えば定義が違うってこともある。
とはいえ,小中高の算数・数学では基本的に定義が変わることはないから安心してね。
あと,定義はルールだから,証明することはできないよ。
定理(theorem)・系(corollary)・原理
証明された命題は定理にランクアップして,有名なものには「○○の定理」って名前もつけられる。
ただ,中高数学でも多くの定理が登場するんだけど,「○○の定理」って名前がつくものは少ない。
名前がつかなかった多くの定理は「性質」や「公式」と呼ばれたり,「名無し」になったり,学校ではあえて定理名を伏せられたりする。
これが混乱を招く原因なんだよね。
ここから下は,ある程度学習が進んだ段階で見直してくれたほうがしっくりくるかも。
定理の詳細(性質・公式・名無し・系・原理)ちなみに,定理に関して気をつけたいことがある。
高校,大学入試においては,記述の際に定理の一部を宣言すべきだということ。
受験する高校,大学次第なんだけど,定理・性質・公式・名無し・原理のうち,高校受験では定理,性質を全て,大学受験では高校で習った名前のある定理,公式,原理を宣言するのが通例になってるんだ。
法則
法則自体は小学校で習うんだけど,数学と自然科学では使われ方が違うことに注意。
具体的には,自然法則,物理法則は「反例が見つかるまでの仮説」で,数学における法則は「演算において成り立つことがある定理の定形」と普通の「定理」がごっちゃになっている。
「演算において成り立つことがある定理の定形」の例
$a$,$b$ を0でない実数とする。
交換法則の定形:$a$○$b=b$○$a$ ※○には演算記号が入る
- 加法の交換法則:$a+b=b+a$ 成り立つ
- 減法の交換法則:$a-b=b-a$ 成り立たない
結合法則の定形:$(a$○$b)$○$c=a$○$(b$○$c)$ ※○には演算記号が入る
- 乗法の結合法則:$a \times b=b \times a$ 成り立つ
- 除法の結合法則:$a \div b=b \div a$ 成り立たない
演算と言われても,中高生は四則演算とベクトルの内積,合同式の演算くらいしか種類がないから実感しづらいかもしれないけど,実際には他にもあって,これらの法則が成り立つかどうかは議論を進める上で重要だったりする。
小中高で習う法則をまとめるとこんな感じ。
■「演算において成り立つことがある定理の定形」としての法則
- 交換法則(commutative law)
- 結合法則(associative law)
- 分配法則(distributive property)
■「定理」としての法則
- ド・モルガンの法則(De Morgan’s laws)
※形式体系によって公理または定理として扱われる - 数え上げの和の法則(rule of sum)
※別名,加法原理 (addition principle) - 数え上げの積の法則(rule of product)
※別名,乗法原理 (multiplication principle) - 大数の法則(law of large numbers)
- 指数法則(Exponents rules)
指数法則は「演算において成り立つことがある定理の定形」に加えてもいいんだけど,中高数学では指数以外に当てはまる演算がないから「定理」に入れておいたよ。
底と指数にどのような数が入るか,という点では定形としての意義もあるけど,実際,指数法則がそのような扱われ方をすることは極めて少ないからね。
勝手にまとめておいてなんだけど,ぶっちゃけ「法則」は全部「定理」。
例えば,交換法則も加法に限定すれば「加法の交換法則」っていう定理になるからね。
そもそも,英語で law,property,rule,principle が混ざっているように,日本語でも「法則」という言葉自体に数学的な定義はないからね。
用語まとめ
- 命題:真偽のはっきりする文章や式
- 公理:最も基本的な仮定,理由なく正しいとされる文章
- 公準:古典的な数学で使われていた公理に準ずる前提(今では公理との区別なし)
- 定義:用語の意味をはっきり述べたもの
- 定理:証明された真の命題
- 性質:定理の呼称方法の一種(数学的な定義なし)
- 公式:数式で表された定理,または,定理に用いられている数式
- 系:定理からすぐに導くことができる定理
- 原理:感覚的,実験的に正しいとされる事柄(数学においては定理の一種)
- 法則:演算において成り立つことがある定理の定形,または,定理
これらの違い,わかってもらえたかな?
ややこしさの原因は数学者の言葉選びのせいだったりするんだけど,基本的には公理,定義,定理に分けられると理解してほしい。
イン数では,これらを扱うときは,
【定義】
○○:○○○○ということ
というように青色で囲むから,この中のことはぜひ覚えてほしい。
第1講のまとめ
最初から堅苦しくなっちゃったけど,数学を学ぶ上で大事なことを凝縮したつもりだから,ここはなんとか乗り越えてほしい。
次回をお楽しみに!