感覚から脱却するタイミング
君は数学を学んでいるとき,どうやって理解しようとしているかな?
① すでに理解している数学以外の事柄に結びつけて理解しようとする
② 数学は数学として区別して理解しようとする
実は,この2つの考え方を自分の中に持っているかどうかが数学ができるかどうかにつながるんだ。
算数では基本的に①で学ぶようになっている。
「3人に4個ずつアメを配ったら全部で何個か?」
そんな日常的,具体的な問いから始まっているよね。
ところが算数,数学を学んでいると,誰でもどこかのタイミングで①ができないタイミングがくる。
それが小学校の「比」なのか,中学校の「負の数」なのか,今までの経験や結びつける力の差によってバラバラではあるけどね。
このタイミングでとる行動はだいたい4つに分けられる。
- ①に固執する。
- ①が無理だと分かっているけど,②をしようとしない。
- ①が無理だと分かっていて,②をしようとするけど,諦めて暗記にはしる。
- ①が無理だと分かったから,②をする。
君はどれかな?
このタイミングで,①のみの考え方から脱却して②を取り入れられるかどうか,つまり,「4」を選べるかどうかが数学の得手不得手を分けるんだ。
早く②を取り入れることで数学を数学として理解しようとする感覚を得ることになるんだけど,その感覚を持たない生徒はよく「分かりやすい説明」として①を欲する。
でも,それは結局自分の理解力を伸ばすことを放棄しているだけだということが分かるかな?
例え話は例えであって本質じゃない。
こういったことをはっきりと教えてくれる先生は少なく,先生に言われるがまま,何も考えずに学んでいる子が多いのは非常に残念だよ。
なぜこのタイミングでこの話をしたかというと,図形というのは一番②を取り入れづらい分野だから。
小学校までは基本的に目で見て分かるようなことしか扱わなかったけど,中高になるとそうではなくなるし,図形を正しく理解して記述するというのはかなりハードルが高いんだ。
だからこそ,意識して②を取り入れないとつまずくことになる。
この講では基本的に言葉で表現することに徹しているけど,それは,図を図としてだけでなく数学的にも理解してほしいから。
実際,これ以降の講ではこの講で学んだ性質が数式に変わっていくんだけど,その説明が「図より」だけでは困るんだよ。
さらにいえば,中学校ではテストでも図を提示してくれるけど,高校になるとそれが一気に減って,文章から図を書き起こすことが増えるしね。
①と②を使いこなして,数学を自分の手足のように操れるようになろう。
平面図形の基本事項
【定義】
直線 $\boldsymbol{\mathrm{AB}}$:2点 $\mathrm{A}$,$\mathrm{B}$ を通る両方向に限りなく伸びている真っ直ぐな線
線分 $\boldsymbol{\mathrm{AB}}$:直線 $\mathrm{AB}$ のうち,点 $\mathrm{A}$ から点 $\mathrm{B}$ までの部分
半直線 $\boldsymbol{\mathrm{AB}}$:直線 $\mathrm{AB}$ のうち,線分 $\mathrm{AB}$ と点 $\mathrm{B}$ の外側の部分
交点:2つの線が交わる点
平面上の2直線 $l$,$m$ が交わらないとき,2直線 $l$,$m$ は平行であるという。
このとき,記号 $/\!/$ を使って $l /\!/ m$ と書き,「$l$ 平行 $m$」と読む。
2直線 $l$,$m$ が交わってできる角が直角であるとき,2直線は垂直であるという。
このとき,記号 $\perp$ を使って $l \perp m$ と書き,「$l$ 垂直 $m$」と読む。
また,2直線が垂直であるとき,一方を他方の垂線という。
2点 $\mathrm{A}$,$\mathrm{B}$ 間の距離:線分 $\mathrm{AB}$ の長さ
点 $\mathrm{P}$ と直線 $l$ の距離:点 $\mathrm{P}$ から直線 $l$ に垂線を引き,その交点を $\mathrm{H}$ としたときの線分 $\mathrm{PH}$ の長さ
平行な2直線 $l$,$m$ の距離:一方の直線上の点と他方の直線との距離(これは常に等しくなる)
中点:線分 $\mathrm{AB}$ 上で,点 $\mathrm{A}$,$\mathrm{B}$ から等しい距離にある点
点 $\mathrm{P}$ が線分 $\mathrm{AB}$ を $m:n$ に内分する:$m$,$n$ を正の数としたとき,線分 $\mathrm{AB}$ 上の点 $\mathrm{P}$ が $\mathrm{AP} : \mathrm{PB} =m:n$ を満たすこと
内分点:内分する点
点 $\mathrm{Q}$ が線分 $\mathrm{AB}$ を $m:n$ に外分する:$m$,$n$ を正の数としたとき,線分 $\mathrm{AB}$ の延長上の点 $\mathrm{Q}$ が $\mathrm{AQ} : \mathrm{QB} =m:n$ を満たすこと
外分点:外分する点
線分 $\mathrm{AB}$ の垂直二等分線:線分 $\mathrm{AB}$ の中点 $\mathrm{M}$ を通り,線分 $\mathrm{AB}$ に垂直な直線
半直線 $\mathrm{BA}$ , $\mathrm{BC}$ によってつくられる角を記号$\angle$ を使って $\boldsymbol{\angle \mathrm{ABC}}$ とかき,「角 $\mathrm{ABC}$」と読む。ただし,他の角と混同することがない場合は $\angle \mathrm{B}$ と表すこともある。
※ $\angle \mathrm{ABC}$ は2つ考えられるが,一般的には小さい方の角を表す。
角の二等分線:1つの角を2等分する半直線
対頂角:2直線が交わってできる4つの角のうち,向かい合った2つの角
同位角:2直線 $l$ , $m$ とこれらに平行でない直線 $n$ があるとき, $l$ , $m$ に対して同じ側,かつ, $n$ に対して同じ側の角
錯角:2直線 $l$ , $m$ とこれらに平行でない直線 $n$ があるとき, $l$ , $m$ の内側,かつ, $n$ に対して反対側の角
三角形 $\boldsymbol{\mathrm{ABC}}$ を,記号 $\triangle$ を使って $\boldsymbol{\triangle \mathrm{ABC}}$ と書く。
$\triangle \mathrm{ABC}$ が式の中で用いられた場合,その面積を表す。
【定理】対頂角の性質
対頂角は等しい。
【定理】平行線と同位角・錯角
同位角または錯角が等しい $\Leftrightarrow$ 2直線は平行
【定理】多角形の内角の和
$n$ 角形の内角の和は $180^{ \circ } \times (n-2)$
【定理】多角形の外角の和
多角形の外角の和は $360^{ \circ }$
数学を勉強していると色々な「分からない」に遭遇するけど,定義,定理を覚えていないというのがその原因の一つ。
特に図形の分野は定義,定理がかなり多いから,しっかり覚えておかないと問題を読み解くことができないんだ。
定義に関しては一つ一つ見れば中身は簡単なはずだから,しっかり読んで,実際に図をかいて理解しよう。
定理に関してはイン数では証明を省いている(今後追加予定)けど,なぜその定理が成り立つのか考えながら理解しよう。
あと,図形の問題文が読めない,分からないというのをよく聞く話で,確かに独特な表現が多いんだけど,それも1つずつ理解していくしかないからね。
以下,図形を考える上で重要な図形の移動についてまとめたよ。
図形の移動
図形の移動:図形の形や大きさを変えずに位置だけを変えること
平行移動:図形を一定の方向に一定の距離だけずらす移動
回転移動:図形を1つの点を中心として一定の角度だけ回転させる移動
回転の中心:回転移動において中心とした点
点対称移動:回転移動のうち1つの点を中心として180° 回転させる移動
対称移動:図形を1つの直線を折り目として折り返す移動
対称軸:対称移動において折り目とした直線
ちなみに,図形はその大きさや形を変えずに移動したり裏返したりできる,というのは公理だからね。
作図
【定義】
作図:定規とコンパスだけを使って図をかくこと
図形について考えるとき当然図をかくんだけど,数学的に正しく図をかくことを作図というんだ。
もちろん,問題を解くときにそこまで正確な図は必要ないからフリーハンドで構わないんだけど,作図を意識するだけで図の出来栄えが全然違ってくるよ。
中学校では「作図せよ」という問題もあるから,作図の基本を抑えておこう。
小学校では定規の目盛りを見て線を引くことができたけど,作図ではそれができないから注意が必要だよ。
定規とコンパスを用いてできること
定規
- 与えられた2点を通る直線(線分)を引くこと
- 線分を延長すること
コンパス
- 与えられた1点を中心として,与えられた半径の円を書くこと
- 直線上に,与えられた線分の長さを移すこと
基本的には定規は線をひくためのもの,コンパスは長さを移すためのものなんだ。
じゃあ「○cmの線分 $\mathrm{AB}$ を引け」と言われたらどうするか?
- 定規で直線を引き,点 $\mathrm{A}$ を決める。
- 定規を使って○cmにコンパスを広げる。
- 点 $\mathrm{A}$ に針をおき,直線と交わる部分に弧をかいて,交わった部分を点 $\mathrm{B}$ とする。
面倒だと思うかもしれないけど,これが正しい作図の仕方なんだ。
正しい作図ができるようになることで,図形のことを正しく理解できるし,図形の性質も徐々に身についていくからおろそかにしないでね。
作図の問題では以下の基本的な作図をよく使うからそれぞれ正しくかけるようになろう。
基本作図
垂線の作図①
直線 $l$ 上にない点 $\mathrm{P}$ を通る,$l$ の垂線の作図
- $l$ 上に適当な2点 $\mathrm{A}$,$\mathrm{B}$ をとり,点 $\mathrm{A}$ を中心として,半径 $\mathrm{AP}$ の円をかく。
- 点 $\mathrm{B}$ を中心として,半径 $\mathrm{BP}$ の円をかく。
- 2円の交点 $\mathrm{P}$,$\mathrm{Q}$ を通る直線を引く。
垂線の作図②
直線 $l$ 上にない点 $\mathrm{P}$ を通る,$l$ の垂線の作図
- 点 $\mathrm{P}$ を中心とする適当な半径の円をかき,直線 $l$ との交点を $\mathrm{A}$,$\mathrm{B}$ とする。
- 2点 $\mathrm{A}$,$\mathrm{B}$ をそれぞれ中心として,等しい半径の円をかき,2つの円の交点の1つを $\mathrm{Q}$ とする。
- 直線 $\mathrm{PQ}$ を引く。
垂直二等分線の作図
線分 $\mathrm{AB}$ の垂直二等分線の作図
- 線分の両端 $\mathrm{A}$,$\mathrm{B}$ をそれぞれ中心として等しい半径の円をかき,2つの円の交点を $\mathrm{P}$,$\mathrm{Q}$ とする。
- 直線 $\mathrm{PQ}$ を引く。
角の二等分線の作図
$∠\mathrm{AOB}$ の二等分線の作図
- 角の頂点 $\mathrm{O}$ を中心として適当な半径の円をかき,半直線 $\mathrm{OA}$,$\mathrm{OB}$ との交点をそれぞれ $\mathrm{P}$,$\mathrm{Q}$ とする。
- 2点 $\mathrm{P}$,$\mathrm{Q}$ をそれぞれ中心として等しい半径の円をかき,この2円の交点の1つを $\mathrm{R}$ とする。
- 半直線 $\mathrm{OR}$ を引く。
図形の合同と相似
【定義】
合同:2つの図形が移動や裏返しによって重ね合わせられること
※$\triangle \mathrm{ABC}$ と $\triangle \mathrm{DEF}$ が合同であることを,記号 $\equiv$ を使って $\triangle \mathrm{ABC} \equiv \triangle \mathrm{DEF}$ とかき,「三角形 $\mathrm{ABC}$ 合同三角形 $\mathrm{DEF}$」と読む。
拡大図:ある図形を一定の割合で拡大した図
縮図:ある図形を一定の割合で縮小した図
相似:2つの図形において,一方の図形を拡大または縮小すると他方の図形と合同になること
※四角形 $\mathrm{ABCD}$ と四角形 $\mathrm{A’B’C’D’}$ が相似であることを,記号 $\backsim$ を使って,四角形 $\mathrm{ABCD} \backsim$ 四角形 $\mathrm{A’B’C’D’}$ と書き,「四角形 $\mathrm{ABCD}$ 相似四角形 $\mathrm{A’B’C’D’}$」と読む。
相似比:相似な図形において対応する線分の長さの比
相似の位置:2つの相似な図形において,対応する点を通る直線が全て1点 $\mathrm{O}$ を通り,点 $\mathrm{O}$ から対応する点までの距離の比がすべて等しくなるような位置関係
相似の中心:相似の位置における点 $\mathrm{O}$
【定理】三角形の合同条件
2つの三角形において
- 3組の辺がそれぞれ等しい。
- 2組の辺とその間の角がそれぞれ等しい。
- 1組の辺とその両端の角がそれぞれ等しい。
のいずれかが成り立つならば,2つの三角形は合同
【定理】直角三角形の合同条件
2つの直角三角形において
- 斜辺と1つの鋭角がそれぞれ等しい
- 斜辺と他の1辺がそれぞれ等しい
のいずれかが成り立つならば,2つの直角三角形は合同
【定理】合同な図形の性質
- 合同な図形において,対応する線分の長さはそれぞれ等しい。
- 合同な図形において,対応する角の大きさはそれぞれ等しい。
【定理】三角形の相似条件
2つの三角形において
- 3組の辺の比がすべて等しい。
- 2組の辺の比とその間の角がそれぞれ等しい。
- 2組の角がそれぞれ等しい。
のいずれかが成り立つならば,2つの三角形は相似
【定理】相似な図形の性質
- 相似な図形において,対応する線分の長さの比はすべて等しい。
- 相似な図形において,対応する角の大きさはそれぞれ等しい。
2つの図形において,移動や裏返しによって重ね合わせられることを合同,一方の図形を拡大または縮小すると他方の図形と合同になることを相似というんだけど,この合同と相似は図形の問題を考える上で欠かせないんだ。
この講に出てくる定理の証明や問題を解くときにもよく使われるからね。
合同条件,相似条件も覚えるだけじゃなくて,なぜこれらが成り立つと合同,相似になるのかも考えてみよう。
例1)
下の図で, $\mathrm{AB} /\!/ \mathrm{CD}$ , $\mathrm{AB} = \mathrm{CD}$ ならば, $\triangle \mathrm{OAB} \equiv \triangle \mathrm{ODC}$ であることを証明せよ。
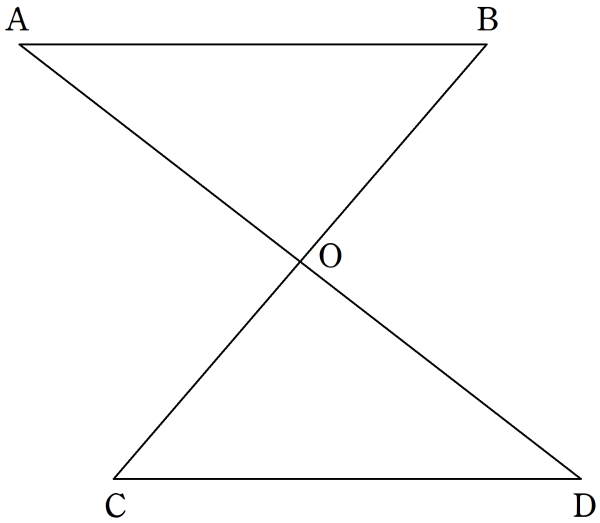
$\triangle \mathrm{OAB}$ と $\triangle \mathrm{ODC}$ において
仮定より
$\mathrm{AB} /\!/ \mathrm{CD}$
$\mathrm{AB} = \mathrm{CD}$ ー①
平行線の錯角は等しいので
$\angle \mathrm{OAB} = \angle \mathrm{ODC}$ ー②
$\angle \mathrm{OBA} = \angle \mathrm{OCD}$ ー③
①,②,③より,1組の辺とその両端の角がそれぞれ等しいので $\triangle \mathrm{OAB} \equiv \triangle \mathrm{ODC}$
例2)
下の図で, $\mathrm{AB} /\!/ \mathrm{CD}$ ならば, $\triangle \mathrm{OAB} \backsim \triangle \mathrm{ODC}$ であることを証明せよ。

$\triangle \mathrm{OAB}$ と $\triangle \mathrm{ODC}$ において
仮定より
$\mathrm{AB} /\!/ \mathrm{CD}$
平行線の錯角は等しいので
$\angle \mathrm{OAB} = \angle \mathrm{ODC}$ ー①
$\angle \mathrm{OBA} = \angle \mathrm{OCD}$ ー②
①,②より,2組の角がそれぞれ等しいので $\triangle \mathrm{OAB} \backsim \triangle \mathrm{ODC}$
例1,2は合同,相似の証明の中学生バージョン。
中学生は証明の練習段階だからかなり丁寧に,詳細に書くのが慣習なんだ。
残念なことに先生独自のルールも多いから注意が必要だよ。
高校生になれば以下の証明で十分。
例1)
$\mathrm{AB} /\!/ \mathrm{CD}$ より
$\angle \mathrm{OAB} = \angle \mathrm{ODC}$ , $\angle \mathrm{OBA} = \angle \mathrm{OCD}$
であり,$\mathrm{AB} = \mathrm{CD}$ であるから $\triangle \mathrm{OAB} \equiv \triangle \mathrm{ODC}$
例2)
$\mathrm{AB} /\!/ \mathrm{CD}$ より
$\angle \mathrm{OAB} = \angle \mathrm{ODC}$ , $\angle \mathrm{OBA} = \angle \mathrm{OCD}$
であるから,$\triangle \mathrm{OAB} \backsim \triangle \mathrm{ODC}$
中高の違いは,定理をどこまで説明するか。
定理を用いるときに仮定と結論を明記するのはどちらも変わらないけど,定理自体を説明する文言については中学生は必要で高校生は不要というのが一般的なんだ。
例えば,中学生バージョンにあった「平行線の錯角は等しい」「1組の辺とその両端の角がそれぞれ等しい」「2組の角がそれぞれ等しい」は高校生バージョンでは省かれているよね?
これらは定理自体の説明だから,仮定と結論からどの定理を用いたか明らかであれば省いても問題ないということ。
まあ,この「明らか」の線引が明らかじゃないんだけどね。
中高の教科書や問題集を見比べてもその違いが分かるはずだし,証明を簡潔に述べるために省くべきかどうかを判断できるようになろう。
とはいえ,これらは慣習にすぎず,大事なのは理論が正しいかどうか。
高校生が中学生バージョンの証明を書いてもまったく問題はないからね。
三角形
【定義】
$\triangle \mathrm{ABC}$ の内角:$\angle \mathrm{A}$,$\angle \mathrm{B}$,$\angle \mathrm{C}$
$\triangle \mathrm{ABC}$ の頂点 $\mathrm{C}$ における外角:直線 $\mathrm{AC}$ 上に,点 $\mathrm{C}$ に関して点 $\mathrm{A}$ と反対側に点 $\mathrm{D}$ を,直線 $\mathrm{BC}$ 上に,点 $\mathrm{C}$ に関して点 $\mathrm{B}$ と反対側に点 $\mathrm{E}$ をとったときの $\angle \mathrm{ACE}$ と $\angle \mathrm{BCD}$
鋭角:$0^{ \circ }$ より大きく $90^{ \circ }$ より小さい角
鈍角:$90^{ \circ }$ より大きく $180^{ \circ }$ より小さい角
鈍角三角形:3つの内角が鋭角である三角形
直角三角形:1つの内角が直角である三角形
鈍角三角形:1つの内角が鈍角である三角形
二等辺三角形:2つの辺が等しい三角形
頂角:二等辺三角形で,長さの等しい2つの辺がつくる角
底辺:頂角に対する辺
底角:底辺の両端の角
正三角形:3つの辺が等しい三角形
最初に習う最もシンプルな多角形だからこそ,三角形に関する定義,定理は非常に多いんだ。
四角形以上の多角形も,三角形の発展として考える部分がたくさんあるから,まずは三角形を理解することに専念しよう。
あと,図形同士の包含関係も一緒に考えると,その図形について正しく理解できるよ。
例えば,正三角形は二等辺三角形に含まれる,直角二等辺三角形は直角三角形と二等辺三角形に含まれる,というようにね。
三角形の種々の定理
【定理】三角形の3辺の長さの性質
1つの三角形において
- 2辺の長さの和は,他の1辺の長さより大きい
- 2辺の長さの差は,他の1辺の長さより小さい。
【定理】三角形の2辺とその向かい合う角の大小関係
$\triangle \mathrm{ABC}$ について
- $a<b \Leftrightarrow A<B$
- $a=b \Leftrightarrow A=B$
- $a>b \Leftrightarrow A>B$
【定理】三角形の成立条件
正の数 $a$,$b$,$c$ に対して
$|b-c|<a<b+c$ $\Leftrightarrow$ 3辺の長さが $a$ , $b$ , $c$ である三角形が存在する
【定理】三角形の辺と角の大小関係
1つの三角形において
- 大きい辺に向かい合う角は,小さい辺に向かい合う各より大きい。
- 大きい角に向かい合う辺は,小さい角に向かい合う辺より大きい。
すなわち $\mathrm{AB} < \mathrm{AC} \Leftrightarrow \angle \mathrm{C} < \angle \mathrm{B}$
【定理】三角形の外角の性質
三角形の外角は,これと隣り合わない2つの内角の和に等しい
【定理】二等辺三角形の性質
- 二等辺三角形の2つの底角は等しい。
- 二等辺三角形の頂角の二等分線は,底辺を垂直に2等分する。
- 2つの角が等しい三角形は二等辺三角形である。
【定理】平行線と比
$\triangle \mathrm{ABC}$ の辺 $\mathrm{AB}$,$\mathrm{AC}$ 上の点をそれぞれ $\mathrm{P}$,$\mathrm{Q}$ とすると,$\mathrm{PQ} /\!/ \mathrm{BC}$ ならば,
- $\mathrm{AP} : \mathrm{AB} = \mathrm{AQ} : \mathrm{AC} = \mathrm{PQ} : \mathrm{BC}$
- $\mathrm{AP} : \mathrm{PB} = \mathrm{AQ} : \mathrm{QC}$
【定理】3本の平行線と線分の比
平行な3直線 $l_1$ , $l_2$ , $l_3$ と,これらに平行でない2直線 $m_1$ , $m_2$ に対して, $m_1$ と $l_1$ , $l_2$ , $l_3$ の交点をそれぞれ $\mathrm{A}$ , $\mathrm{B}$ , $\mathrm{C}$ , $m_2$ と $l_1$ , $l_2$ , $l_3$ の交点をそれぞれ $\mathrm{D}$ , $\mathrm{E}$ , $\mathrm{F}$ とすると,
$\mathrm{AB} : \mathrm{BC} = \mathrm{DE} : \mathrm{EF}$
【定理】比と平行線
$\triangle \mathrm{ABC}$ の辺 $\mathrm{AB}$,$\mathrm{AC}$ 上の点をそれぞれ $\mathrm{P}$,$\mathrm{Q}$ とすると,
- $\mathrm{AP} : \mathrm{AB} = \mathrm{AQ} : \mathrm{AC}$ ならば,$\mathrm{PQ} /\!/ \mathrm{BC}$
- $\mathrm{AP} : \mathrm{PB} = \mathrm{AQ} : \mathrm{QC}$ ならば,$\mathrm{PQ} /\!/ \mathrm{BC}$
【定理】中点連結定理
$\triangle \mathrm{ABC}$ の辺 $\mathrm{AB}$,$\mathrm{AC}$ の中点をそれぞれ $\mathrm{M}$,$\mathrm{N}$ とすると,
$\mathrm{MN} /\!/ \mathrm{BC}$,$\mathrm{MN} = \displaystyle{\frac{1}{2}} \mathrm{BC}$
【定理】平行線と同位角・錯角,辺の比
$\triangle \mathrm{ABC}$ の辺 $\mathrm{AB}$ 上に点 $\mathrm{P}$ があり,辺 $\mathrm{AC}$ 上に点 $\mathrm{Q}$ があるとき
- $\mathrm{PQ} /\!/ \mathrm{BC} \Leftrightarrow \mathrm{AP} : \mathrm{AB} = \mathrm{AQ} : \mathrm{AC}$
- $\mathrm{PQ} /\!/ \mathrm{BC} \Leftrightarrow \mathrm{AP} : \mathrm{PB} = \mathrm{AQ} : \mathrm{QC}$
- $\mathrm{PQ} /\!/ \mathrm{BC} \Leftrightarrow \mathrm{AP} : \mathrm{AB} = \mathrm{PQ} : \mathrm{BC}$
【定理】三角形の内角の二等分線と辺の比
$\triangle \mathrm{ABC}$ の $\angle \mathrm{A}$ の二等分線と辺 $\mathrm{BC}$ との交点 $\mathrm{P}$ は,辺 $\mathrm{BC}$ を $\mathrm{AB} : \mathrm{AC}$ に内分する。
【定理】三角形の外角の二等分線と辺の比
$\mathrm{AB} \neq \mathrm{AC}$ である $\triangle \mathrm{ABC}$ の頂点 $\mathrm{A}$ における外角の二等分線と辺 $\mathrm{BC}$ の延長との交点 $\mathrm{Q}$ は,辺 $\mathrm{BC}$ を $\mathrm{AB} : \mathrm{AC}$ に外分する。
【定理】チェバの定理
$\triangle \mathrm{ABC}$ の3頂点 $\mathrm{A}$,$\mathrm{B}$,$\mathrm{C}$ と,三角形の辺上にもその延長上にもない点 $\mathrm{O}$ を結ぶ直線が,辺 $\mathrm{BC}$,$\mathrm{CA}$,$\mathrm{AB}$ またはその延長と交わるとき,交点をそれぞれ $\mathrm{P}$,$\mathrm{Q}$,$\mathrm{R}$ とすると
$\displaystyle \frac{\mathrm{BP}}{\mathrm{PC}} \cdot \frac{\mathrm{CQ}}{\mathrm{QA}} \cdot \frac{\mathrm{AR}}{\mathrm{RB}} =1$
【定理】チェバの定理の逆
$\triangle \mathrm{ABC}$ の辺 $\mathrm{BC}$,$\mathrm{CA}$,$\mathrm{AB}$ またはその延長上にそれぞれ点 $\mathrm{P}$,$\mathrm{Q}$,$\mathrm{R}$ があり,この3点のうちの1個または3個が辺上にあるとする。このとき,$\mathrm{BQ}$ と $\mathrm{CR}$ が交わり,かつ
$\displaystyle \frac{\mathrm{BP}}{\mathrm{PC}} \cdot \frac{\mathrm{CQ}}{\mathrm{QA}} \cdot \frac{\mathrm{AR}}{\mathrm{RB}} =1$
が成り立つならば,3直線 $\mathrm{AP}$,$\mathrm{BQ}$,$\mathrm{CR}$ は1点で交わる。
【定理】メネラウスの定理
$\triangle \mathrm{ABC}$ の辺 $\mathrm{BC}$,$\mathrm{CA}$,$\mathrm{AB}$ またはその延長が,三角形の頂点を通らない1つの直線とそれぞれ点 $\mathrm{P}$,$\mathrm{Q}$,$\mathrm{R}$ で交わるとき
$\displaystyle \frac{\mathrm{BP}}{\mathrm{PC}} \cdot \frac{\mathrm{CQ}}{\mathrm{QA}} \cdot \frac{\mathrm{AR}}{\mathrm{RB}} =1$
【定理】メネラウスの定理の逆
$\triangle \mathrm{ABC}$ の辺 $\mathrm{BC}$,$\mathrm{CA}$,$\mathrm{AB}$ またはその延長上に,それぞれ点 $\mathrm{P}$,$\mathrm{Q}$,$\mathrm{R}$ があり,この3点のうちの1個または3個が辺の延長上にあるとする。このとき
$\displaystyle \frac{\mathrm{BP}}{\mathrm{PC}} \cdot \frac{\mathrm{CQ}}{\mathrm{QA}} \cdot \frac{\mathrm{AR}}{\mathrm{RB}} =1$
が成り立つならば,3点 $\mathrm{P}$,$\mathrm{Q}$,$\mathrm{R}$ は1つの直線上にある。
求値問題にせよ証明問題にせよ,どうしたら結論に結びつくかという逆算の考え方がとても重要なんだ。
定理が多いということは使える手札が多いということなんだけど,それだけどれを使うべきなのか迷うということ。
パターン暗記では絶対に応用力は伸びないから,仮定と結論を見極めて,構成をどうするか考えながら問題を解く練習をしよう。
図形に限らず,数学では別解があることが多いから,色々な解法を検証することで,定理の使い所を身に着けていくといいよ。
三角形の五心
【定義】
外接円:三角形の3つの頂点を通る円
外心:外接円の中心
内接円:三角形の3辺に接する円
内心:内接円の中心
中線:三角形の頂点と向かい合う辺の中点を結ぶ線分
重心:三角形の3本の中線の交点
垂心:三角形の3つの頂点から向かい合う辺に下ろした垂線の交点
傍接円:三角形の1辺と他の2辺の延長に接する円
傍心:傍接円の中心
※傍心・傍接円は3つある。
【定理】三角形の五心
- 三角形の3辺の垂直二等分線は1点で交わる。(外心)
- 三角形の3つの内角の二等分線は1点で交わる。(内心)
- 三角形の3本の中線は1点で交わり,その点は各中線を $2:1$ に内分する。(重心)
- 三角形の3つの頂点から向かい合う辺に下ろした垂線1点で交わる。(垂心)
- 三角形の1つの頂点における内角の二等分線と,他の2つの頂点における外角の二等分線は1点で交わる。(傍心)
三角形には重心だけじゃなくて,他にも4つの心があるんだ。
証明する前にまずは作図をしてみて,その不思議さを味わってほしいな。
四角形
【定義】
対辺:四角形の向かい合う辺
対角:四角形の向かい合う角
台形:1組の対辺が平行な四角形
等脚台形:底辺の両端の内角が等しい台形
平行四辺形:2組の対辺がそれぞれ平行な四角形
平行四辺形 $\mathrm{ABCD}$ を,記号 ▱ を使って ▱ $\mathrm{ABCD}$ と書く。
長方形:4つの角が等しい四角形
ひし形:4つの辺が等しい四角形
正方形:4つの角が等しく,4つの辺が等しい四角形
【定理】平行四辺形になるための条件
- 2組の対辺がそれぞれ平行である
- 2組の対辺がそれぞれ等しい
- 2組の対角がそれぞれ等しい
- 2つの対角線がそれぞれの中点で交わる
- 1組の対辺が平行で等しい
【定理】平行四辺形の性質
- 2組の対辺はそれぞれ等しい
- 2組の対角はそれぞれ等しい
- 2つの対角線はそれぞれの中点で交わる
四角形の中で特に注目したいのが平行四辺形。
中高で扱う平行四辺形の定義としては「2組の対辺がそれぞれ平行な四角形」なんだけど,定理「平行四辺形になるための条件」を見て分かる通り,定義以外にも平行四辺形になる条件はたくさんあるんだ。
当然これらは同値だから,この条件のうちの1つを定義にしても本質的には問題ないんだよ。
平行四辺形の証明問題や平行四辺形を用いて何かを求めるような問題では,わざわざ定義まで誘導しなくても条件のうちどれかを満たせばいい,ということを念頭に置こう。
さて,ここまでで多角形は終わり。
中高数学では五角形以上の多角形を特別に扱うことはないから,問題で登場したら三角形や四角形に落とし込んで考えるようにしよう。
円
【定義】
弧:円弧の一部分
※2点 $\mathrm{A}$,$\mathrm{B}$ を両端とする弧を,記号 $\stackrel{ \Large \frown }{\mathrm{ }}$ を使って $\stackrel{ \Large \frown }{\mathrm{AB}}$ と書き,「弧 $\mathrm{AB}$」と読む。
弦:円周上の2点を結ぶ線分
扇形:2つの半径と弧で囲まれた図形
中心角:扇形で,2つの半径の作る角
円と直線が接する:円と直線が1点だけを共有すること
接点:共有する点
接線:接する直線
多角形が円に内接する:多角形のすべての頂点が1つの円周上にあること
外接円:多角形のすべての頂点を通る円
点 $\mathrm{O}$ を中心とする円 $\mathrm{O}$ の $\stackrel{ \Large \frown }{\mathrm{AB}}$ と,$\stackrel{ \Large \frown }{\mathrm{AB}}$ を除いた円周上の点 $\mathrm{P}$ に対して,
$\stackrel{ \Large \frown }{\mathrm{AB}}$ に対する円周角:$\angle \mathrm{APB}$
$\stackrel{ \Large \frown }{\mathrm{AB}}$ に対する中心角:$\angle \mathrm{AOB}$
接線や円周角等の新しい用語に加えて,すべての円は相似だということもおさえておこう。
円の種々の定理
【定理】円周角の定理
- 1つの弧に対する円周角は,その弧に対する中心角の半分である。
- 1つの弧に対する円周角はすべて等しい。
- 半円の弧に対する円周角は $90^{ \circ }$ である。
【定理】円周角の定理の逆
2点 $\mathrm{P}$,$\mathrm{Q}$ が直線 $\mathrm{AB}$ について同じ側にあるとき
$\angle \mathrm{APB} = \angle \mathrm{AQB}$ $\Rightarrow$ 4点 $\mathrm{A}$,$\mathrm{P}$,$\mathrm{Q}$,$\mathrm{B}$ は1つの円周上にある
【定理】弧と円周角
1つの円,または半径の等しい円において
- 等しい弧に対する円周角は等しい。
- 等しい円周角に対する弧は等しい。
【定理】円の内部・外部の点と角の大小
円の周上に3点 $\mathrm{A}$,$\mathrm{Q}$,$\mathrm{B}$ があり,点 $\mathrm{P}$ が直線 $\mathrm{AB}$ に関して点 $\mathrm{Q}$ と同じ側にあるとき
- 点 $\mathrm{P}$ が円の周上にある $\Rightarrow$ $\angle \mathrm{APB} = \angle \mathrm{AQB}$
- 点 $\mathrm{P}$ が円の内部にある $\Rightarrow$ $\angle \mathrm{APB} > \angle \mathrm{AQB}$
- 点 $\mathrm{P}$ が円の外部にある $\Rightarrow$ $\angle \mathrm{APB} < \angle \mathrm{AQB}$
【定理】円に内接する四角形
四角形が円に内接するとき
- 四角形の対角の和は $180^{ \circ }$ である。
- 四角形の外角は,それと隣り合う内角の対角に等しい。
【定理】円に内接する四角形の逆
四角形において
- 1組の対角の和が $180^{ \circ }$ である。
- 1つの外角が,それと隣り合う内角の対角に等しい。
これらのどちらかが成り立つ四角形は円に内接する。
※円に内接する四角形とその逆を合わせて
円に内接する四角形 $\Leftrightarrow$ $(内角)+(対角)=180^{ \circ }$ または $(内角)=(対角の外角)$
【定理】円と接線
- 円 $\mathrm{O}$ の周上の点 $\mathrm{A}$ を通る直線 $l$ について
直線 $l$ が点 $\mathrm{A}$ で円 $\mathrm{O}$ に接する $\Leftrightarrow$ $\mathrm{OA} \perp l$
が成り立つ。 - 円の外部の点から円に引くことができる接線は2本ある。
- 円の外部の点から円に接線を引いたとき,外部の点と接点の間の距離を接線の長さという。
- 円の外部の1点 $\mathrm{P}$ からその円に引いた2本の接線の長さは等しい。
【定理】接弦定理
円 $\mathrm{O}$ の弦 $\mathrm{AB}$ と,その端点 $\mathrm{A}$ における接線 $\mathrm{AT}$ が作る角 $\angle \mathrm{BAT}$ は,その角の内部に含まれる $\stackrel{ \Large \frown }{\mathrm{AB}}$ に対する円周角 $\angle \mathrm{ACB}$ に等しい。
【定理】接弦定理の逆
円 $\mathrm{O}$ の $\stackrel{ \Large \frown }{\mathrm{AB}}$ と半直線 $\mathrm{AT}$ が直線 $\mathrm{AB}$ の同じ側にあって,$\stackrel{ \Large \frown }{\mathrm{AB}}$ に対する円周角 $\angle \mathrm{ACB}$ が $\angle \mathrm{BAT}$ に等しいとき,直線 $\mathrm{AT}$ は点 $\mathrm{A}$ で円 $\mathrm{O}$ に接する。
【定理】方べきの定理Ⅰ
円の2つの弦 $\mathrm{AB}$,$\mathrm{CD}$ の交点,またはそれらの延長の交点を $\mathrm{P}$ とすると $\mathrm{PA} \cdot \mathrm{PB} = \mathrm{PC} \cdot \mathrm{PD}$ が成り立つ。
※円の中心を $\mathrm{O}$,半径を $r$ とすると $\mathrm{PA} \cdot \mathrm{PB} =| \mathrm{OP}^2-r^2|$
【定理】方べきの定理Ⅱ
円の外部の点 $\mathrm{P}$ から円に引いた接線の接点を $\mathrm{T}$ とする。点 $\mathrm{P}$ を通ってこの円と2点 $\mathrm{A}$,$\mathrm{B}$ で交わる直線を引くと $\mathrm{PA} \cdot \mathrm{PB} = \mathrm{PT}^2$ が成り立つ。
【定理】方べきの定理の逆
2つの線分 $\mathrm{AB}$ と $\mathrm{CD}$,または $\mathrm{AB}$ の延長と $\mathrm{CD}$ の延長が点 $\mathrm{P}$ で交わるとき,$\mathrm{PA} \cdot \mathrm{PB} = \mathrm{PC} \cdot \mathrm{PD}$ が成り立つならば,4点 $\mathrm{A}$,$\mathrm{B}$,$\mathrm{C}$,$\mathrm{D}$ は1つの円周上にある。
円に関する定理はこれだけあるんだけど,多角形の定理に比べて実感しづらいんじゃないかな?
証明すれば納得はできるんだけど,見た目から想像しづらいというか,直感が働きづらいというか。
もしそうなら,自分の中にすべての定理が選択肢として残せるよう,証明して,たくさん使って習得しよう。
2つの円の位置関係と共通接線
【定義】
共通接線:2つの円に接している直線
共通内接線:2つの円が両側にある共通接線
共通外接線:2つの円が同じ側にある共通接線
2円の位置関係
半径がそれぞれ $r$,$r’$ ( $r>r’$ )である2つの円の中心間の距離を $d$ とすると,2つの円の位置関係は5種類に分けられ,それによって共通接線の本数が定まる。
| 位置関係 | 一方が他方の内部にある | 内接する | 2点で交わる | 外接する | 一方が他方の外部にある |
| 条件 | $d<r-r’$ | $d=r-r’$ | $r-r'<d<r+r’$ | $d=r+r’$ | $d>r+r’$ |
| 共通内接線の本数 | 0 | 0 | 0 | 1 | 2 |
| 共通外接線の本数 | 0 | 1 | 2 | 2 | 2 |
| 共通接線の本数 | 0 | 1 | 2 | 3 | 4 |
※2つの円が接するとき,この共有点を接点といい,接点は2つの円の中心を結ぶ直線上にある。
共通接線も2円の位置関係も図は非常に単純なものなんだけど,それぞれの状態を言葉や式で表現できるかな?
上の2円の位置関係でいえば,「半径がそれぞれ $r$,$r’$ ( $r>r’$ )である2つの円の中心間の距離を $d$ とすると,$r-r'<d<r+r’$ のとき2つの円は2点で交わる」というのが図とちゃんとリンクしているか,ということ。
これを身につけないと,これ以降の講で確実に躓くことになるよ。
小学校までは図形が得意な子が多いけど,中学校以降は苦手な子が一気に増えるのはこのせいなんだ。
平面図形の問題
角度と比(長さ)を求める問題のポイント
| キーワード | 解法 |
| 外心 | 二等辺三角形 |
| 内心 | 角の二等分線 |
| 円に内接,四角形 | 円に内接する四角形 |
| 円,接線 | 接弦定理 |
| 角の二等分線,内心 | 内角,外角の二等分線と辺の比 |
| 重心 | 3本の中線は重心によって $2:1$ に内分される |
| 三角形,分点 | チェバの定理,メネラウスの定理 |
| 円,直線,接線 | 方べきの定理 |
問題をたくさん解けばこんなもの必要ないんだけど,最初にもいった通り図形では定理が多いから,自分の中に選択肢として準備するだけじゃなく,ある程度はそれを絞り込む条件を覚えておくのをおすすめするよ。
この講だけでも40個以上の定理があるからね。
空間図形の基本事項
【定義】
ねじれの位置:空間内で,2直線が平行でなく,交わらないという位置関係 $\Leftrightarrow$ 空間内で,2直線が同一平面上にないという位置関係
直線 $l$ と平面 $\mathrm{P}$ が交わらないとき,直線 $\boldsymbol{l}$ と平面 $\boldsymbol{ \mathrm{P} }$ は平行であるといい,$l /\!/ \mathrm{P}$とかく。
直線 $l$ が平面 $\mathrm{P}$ と点 $\mathrm{O}$ で交わり,点 $\mathrm{O}$ を通る平面 $\mathrm{P}$ 上のすべての直線と垂直であるとき,直線 $\boldsymbol{l}$ と平面 $\boldsymbol{ \mathrm{P} }$ は垂直であるといい,$l \perp \mathrm{P}$ とかく。このとき,直線 $\boldsymbol{l}$ を平面 $\boldsymbol{ \mathrm{P} }$ の垂線という。
2平面 $\mathrm{P}$,$\mathrm{Q}$ が交わらないとき,平面 $\boldsymbol{ \mathrm{P} }$ と平面 $\boldsymbol{ \mathrm{Q} }$ は平行であるといい,$\mathrm{P} /\!/ \mathrm{Q}$ とかく。
2平面 $\mathrm{P}$,$\mathrm{Q}$ が交わってできる直線を交線という。
2平面 $\mathrm{P}$,$\mathrm{Q}$ が交わるとき,その交線 $l$ 上に点 $\mathrm{A}$ をとり,平面 $\mathrm{P}$ 上に$\mathrm{AB} \perp l$,平面 $\mathrm{Q}$ 上に $\mathrm{AC} \perp l$ となる半直線 $\mathrm{AB}$,$\mathrm{AC}$ を引く。このとき,$∠ \mathrm{BAC} =90°$ ならば,平面 $\boldsymbol{ \mathrm{P} }$ と平面 $\boldsymbol{ \mathrm{Q} }$ は垂直であるといい,$\mathrm{P} \perp \mathrm{Q}$ とかく。
点 $\boldsymbol{ \mathrm{A} }$ と平面 $\boldsymbol{ \mathrm{P} }$ の距離:平面 $\mathrm{P}$ 上にない点 $\mathrm{A}$ から $\mathrm{P}$ へ引いた垂線 $\mathrm{AH}$ の長さ
【定理】平面の決定条件
- 同一直線上にない3点
- 1直線と,その上にない1点
- 交わる2直線
- 相異なる平行な2直線
【定理】直線と面の垂直
- 平行な2直線の一方に垂直な直線は他方にも垂直である。
- 直線 $l$ が平面 $\alpha$ 上の交わる2直線 $m$,$n$ に垂直ならば,直線 $l$ は平面 $\alpha$ に垂直である。
- 平面 $\alpha$ の垂線を含む平面は平面 $\alpha$ に垂直である。
【定理】三垂線の定理
平面 $\alpha$ とその上に直線 $l$ があるとき,平面 $\alpha$ 上にない点 $\mathrm{A}$,平面 $\alpha$ 上にあるが直線 $l$ 上にない点 $\mathrm{O}$,直線 $l$ 上に点 $\mathrm{B}$ について
- $\mathrm{OA} \perp \alpha$,$\mathrm{OB} \perp l$ $\Rightarrow$ $\mathrm{AB} \perp l$
- $\mathrm{OA} \perp \alpha$,$\mathrm{AB} \perp l$ $\Rightarrow$ $\mathrm{OB} \perp l$
- $\mathrm{OB} \perp l$,$\mathrm{AB} \perp l$,$\mathrm{OA} \perp \mathrm{OB}$ $\Rightarrow$ $\mathrm{OA} \perp \alpha$
ここからは空間図形を扱うけど,平面図形よりも考えることが増えてややこしくなるから,まずは空間における直線と面の位置関係についてまとめておくよ。
ポイントは,共有点があるかないかという切り口で考えること。
視覚的にも実感してほしいから,下敷き(面)と鉛筆(直線)等を使ってそれぞれの位置関係を自分で再現してみよう。
2直線の位置関係
異なる2直線 $l$,$m$ の位置関係には次の3つの場合がある。
- 1点で交わる。
※共有点が1つある,かつ,1つの平面上にある - 平行である。
※共有点がない,かつ,1つの平面上にある
※2直線 $l$ , $m$ が平行であることを $l /\!/ m$ とかく - ねじれの位置にある。
※共有点がない,かつ,1つの平面上にない
まず,「1点で交わる」と「平行」は1つの平面上にある状態だから考え方は平面と同じだよ。
3直線 $l$ , $m$ , $n$ について,$l /\!/ m /\!/ n$ $\Rightarrow$ $l /\!/ n$ が成り立つのも平面と同じ。
ただ, $l$ と $m$ , $m$ と $n$ , $n$ と $l$ は同じ平面上にあるといえるけど,3直線すべてが同じ平面上にあるとは限らない点に注意してね。
次に,平面にはなかった「ねじれの位置」なんだけど,これは2直線が同じ平面上にない,ということなんだ。
2直線が交わりもしないし平行でもない,ともいえるね。
続いて,2直線 $l$ , $m$ が平行でないとき,任意の1点 $\mathrm{O}$ を通って $l$,$m$ に平行な直線をそれぞれ $l’$,$m’$ とすると,$l’$ と $m’$ は1つの平面上にあって,このとき $l’$ と $m’$ のなす2つの角は点 $\mathrm{O}$ をどこにとっても一定で,この角を2直線 $l$,$m$ のなす角というんだ。
2直線が交わっているときのなす角は分かりやすいけど,ねじれの位置にあるときもなす角はあるからね。
あと,なす角は2つできるんだけど,問題では大きい方,小さい方という指定があることがほとんどだよ。
加えて,2直線 $l$,$m$ のなす角が直角のとき, $l$ と $m$ は垂直であるといい,$l \perp m$ とかき,垂直な2直線 $l$ と $m$ が交わるとき,$l$ と $m$ は直交するというんだ。
2直線がねじれの位置にあるとき,垂直になることはあっても直交することはない,ということだね。
直線と平面の位置関係
直線 $l$ と平面 $\alpha$ の位置関係には次の3つの場合がある。
- $l$ は $\alpha$ に含まれる。($l$ は $\alpha$ 上にある)
※共有点が無数にある - 1点で交わる。
※共有点が1つある - 平行である。
※共有点がない
※直線 $l$ と平面 $\alpha$ が平行であることを $l /\!/ \alpha$ とかく
2直線の位置関係よりはそれぞれイメージしやすいんじゃないかな。
直線の平面の位置関係で特別なのは,角の考え方。
直線 $l$ が,平面 $\alpha$ 上のすべての直線に垂直であるとき,$l$ は $\alpha$ に垂直である,または,$l$ は $\alpha$ に直交するといって $l \perp \alpha$ とかき,直線 $l$ を平面 $\alpha$ の垂線というんだ。
2直線の位置関係のなす角のように垂直以外の角は考えないよ。
2平面の位置関係
異なる2平面 $\alpha$,$\beta$ の位置関係には,次の2つの場合がある。
- 交わる。
※共有点が無数にある - 平行である。
※共有点がない
※2平面 $\alpha$,$\beta$ が平行であることを $\alpha /\!/ \beta$ とかく
2平面が交わるとき,その交わりは直線になって,その直線を交線といい,交わる2平面の交線上の点から,各平面上で交線に垂直に引いた2直線のなす角を2平面のなす角というんだ。
2平面 $\alpha$,$\beta$ のなす角が直角のとき,$\alpha$ と $\beta$ は垂直である,または,直交するといい,$\alpha \perp \beta$ とかくよ。
空間図形
【定義】
柱体:合同で平行な二つの平面図形を底面としてもつ立体
直柱体:底面と側面が直行している柱体
斜柱体:底面と側面が直行していない柱体
角柱:底面が多角形の柱体
正多角柱:底面が正多角形の直柱体
錐体:平面上にある図形の周上の各点と,その平面外の一点とを結んでできる立体
直錐体:頭頂点から底面におろした垂線の足が底面の重心に一致する錐体
斜錐体:頭頂点から底面におろした垂線の足が底面の重心に一致しない錐体
※直錐体,斜錐体であることを表すために,直○○錐,斜〇〇錐とかくことがある
角錐:底面が多角形の錐体
※底面の形によって,三角錐,四角錐,…という
※底面に含まれない点を頭頂点という
円錐:底面が円の錐体
正多角錐:底面が正多角形の直錐体
回転体:平面図形を,同じ平面上の直線 $l$ を軸として1回転してできる立体
母線:円錐の場合は頂点と底面の周上の点の線分,円柱の場合は,側面に回転の軸と平行に2つの底面の間に引いた線分
多面体:平面だけで囲まれている立体で,その面の数によって四面体,五面体,…という
凸多面体:へこみのない多面体
正多面体:すべての面が合同な正多角形で,どの頂点にも面が同じ数だけ集まり,へこみのない多面体
※正多面体は,正四面体,正六面体(立方体),正八面体,正十二面体,正二十面体の5種類しかない。
投影図:立体を正面と真上から見た図で表す方法
立面図:投影図で,立体を正面から見てかいた図
平面図:投影図で,立体を真上から見てかいた図
※立面図と平面図だけでその立体をはっきり表すことができない場合は,真横から見た図を加えて表すことがある。
※立体を平面上の図で表す方法には,他に見取図や展開図がある。
【定理】オイラーの多面体定理
凸多面体の頂点の数を $v$,辺の数を $e$,面の数を $f$ とすると
$v-e+f=2$
が成り立つ。
いよいよ空間図形,といいつつ,空間図形では図形ごとの定理というのはほとんどないんだ。
次の講で体積や表面積を扱うから,それまでにしっかり図形を区別できるようになろう。
第10講のまとめ
定義,定理が盛りだくさんだったけど,諦めず,理解しようとしてくれたかな?
正しく理解するということは正しく説明できるようになること。
何度でも読み返して,図をかいて,数学的な感覚を習得していってほしいな。
この講では図形の性質に終始したけど,次の講では図形を計量,つまり,長さや面積を具体的に求める操作を学んでいくよ。


