二項分布の正規分布による近似を,より精密にすることを考えると以下のようになる。
例えば,$X$ が二項分布 $B(16,0.5)$ に従うとき,$X$ の期待値 $m$ と標準偏差 $\sigma$ は
$m=np=16\times0.5=8$
$\sigma=\sqrt{npq}=\sqrt{16\times0.5\times0.5}=2$
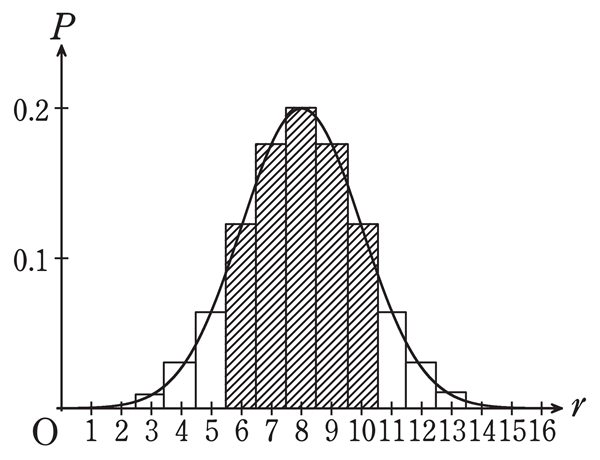
上図は $r=0,1,\cdots\cdots,16$ に対して,$P(X=r)$ の値を,$r$ を底辺の中心とする幅 $1$ の長方形の面積で表したもので,図の曲線は $N(8,2^2)$ に従う確率変数 $Y$ の確率密度関数のグラフである。
このとき,確率 $P=P(6\leqq X\leqq10)$ は図の斜線部分の面積であるから,図からわかるように $P\fallingdotseq P(5.5\leqq Y\leqq10.5)$ である
$Z=\displaystyle\frac{Y-8}{2}$ とすると,$Z$ は標準正規分布 $N(0,1)$ に従うから
$\displaystyle{P\fallingdotseq P\left(\frac{5.5-8}{2}\leqq \frac{Y-8}{2}\leqq\frac{10.5-8}{2}\right)=2p(1.25)=0.7888}$
このように, $6$ と $10$ を $5.5$ と $10.5$ で置き換えることを半整数補正または連続補正という。
半整数補正を行わないで
$\displaystyle{P\fallingdotseq P(6\leqq Y\leqq10)=P\left(\frac{6-8}{2}\leqq\frac{Y-8}{2}\leqq\frac{10-8}{2}\right)=0.6826}$
とすると,両端の長方形のほぼ半分を除いたことになる。二項分布から直接 $P(6\leqq Y\leqq10)$ を計算すると
$({}_16 \mathrm{ C }_6+{}_16 \mathrm{ C }_7+{}_16 \mathrm{ C }_8+{}_16 \mathrm{ C }_9+{}_16 \mathrm{ C }_10)\times0.5^{16}=0.78988\cdots\cdots$
である。
二項分布 $B(n,p)$ の正規近似の精度は,$p$ が $0.5$ に近いほどよく,$p$ が $0$ や $1$ に近いほど悪いが,半整数補正を行った場合,$np$ と $n(1-p)$ がともに $5$ より大きいと実用上十分であると言われている。半整数補正を行わないときは,$np$ と $n(1-p)$ がかなり大きくないと,よい近似が得られない。
