【定義・定理・公式】中学数学基本事項 – 3年生 – 平行線と相似

平行線と比

【定理】

平行線と比

$\triangle \mathrm{ABC}$ の辺 $\mathrm{AB}$，$\mathrm{AC}$ 上の点をそれぞれ $\mathrm{P}$，$\mathrm{Q}$ とすると，$\mathrm{PQ} /\!/ \mathrm{BC}$ ならば，

$\mathrm{AP} : \mathrm{AB} = \mathrm{AQ} : \mathrm{AC} = \mathrm{PQ} : \mathrm{BC}$

$\mathrm{AP} : \mathrm{PB} = \mathrm{AQ} : \mathrm{QC}$

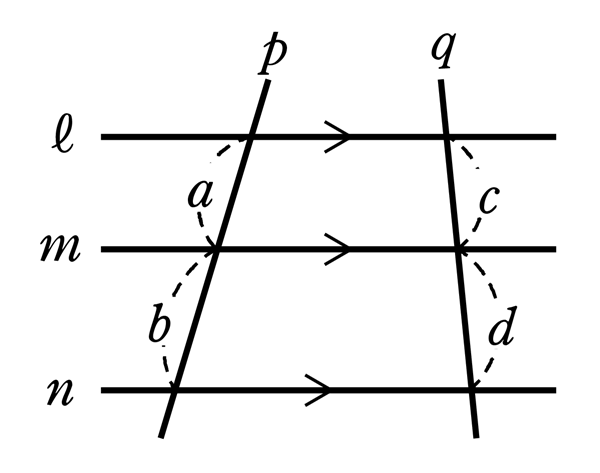
$l /\!/ m /\!/ n$ のとき，$a:c=b:d$

【定理】

比と平行線

$\triangle \mathrm{ABC}$ の辺 $\mathrm{AB}$，$\mathrm{AC}$ 上の点をそれぞれ $\mathrm{P}$，$\mathrm{Q}$ とすると，

$\mathrm{AP} : \mathrm{AB} = \mathrm{AQ} : \mathrm{AC}$ ならば，$\mathrm{PQ} /\!/ \mathrm{BC}$

$\mathrm{AP} : \mathrm{PB} = \mathrm{AQ} : \mathrm{QC}$ ならば，$\mathrm{PQ} /\!/ \mathrm{BC}$

【定理】

中点連結定理

$\triangle \mathrm{ABC}$ の辺 $\mathrm{AB}$，$\mathrm{AC}$ の中点をそれぞれ $\mathrm{M}$，$\mathrm{N}$ とすると，

$\mathrm{MN} /\!/ \mathrm{BC}$，$\mathrm{MN} = \displaystyle{\frac{1}{2}} \mathrm{BC}$